
一、前言
最近因為對幾何有點興趣,所以一直在網路上搜尋相關的資訊。這些資訊裏頭,我比較喜歡看關於證明的部分。為什麼呢?雖然冗長的證明要看的懂,必須得絞盡腦汁,一不小心就會睡著了;但是,比起單純背公式、然後演算、演算再演算的過程(像是從小學到高中,甚至有些人到了大學還是得如此;應該能了解那種無聊吧?),去證明一個題目有趣多了。
二、海龍公式
見下圖
三、解法
一般接觸到海龍公式,都是在高中的時候。大概是談到三角函數那邊的時候吧,海龍在最後一小結發出怒吼、咆嘯而出,嚇得學生措手不及。雖然大家都知道三角形的面積是 底 * 高 / 2 ,但要把面積公式透過餘弦定理、兩次平方差公式,轉換成海龍公式,總是不太直覺。(甚至有點硬掰的感覺)
海龍公式是一個叫做海倫(Heron 或 Hero of Alexandria,1-75 AD)的數學家發明的(廢話= =)。他不僅僅只是古希臘時期的數學家,同時也是力學家與機械學家,比歐幾里得晚了約 350 年左右。

海龍是從《測量術》(Metrica)這本書裏頭被我們給喚醒的。顧名思義,這本書是個實用的測量手冊;但由於當時的時代數的概念尚未發展完全,所以主要是以幾何的方式描述數學問題。海倫利用了內切圓作圖、相似三角形等方式,得到了海龍公式。
至於第三種方式呢,則是利用商高定理。和利用餘弦定理證明海龍公式有點類似,同樣是利用 底 * 高 / 2 ,將三角形的高替換成有辦法求得的已知數。以下圖為例,就是想辦法把 線段 AD 用已知數表達出來。(感覺也有點硬湊)
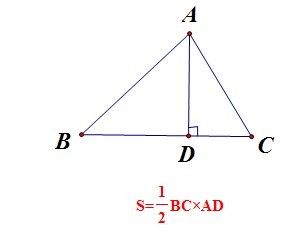
四、小結
因為個人的數學能力不足、以及數學符號不好呈現的緣故,就不在此作推導了。但網路上許多海龍公式的推導過程,就蒐集一些貼在文章的尾巴,做個結束。
解法
- 商高定理解法
-
幾何解法
-
餘弦 + 幾何解法

沒有留言:
張貼留言